从数学角度论证和解释 Uniswap 创始人与 Paradigm 研究团队设计的全新做市模型 TWAMM 的工作原理。
撰文:luffy
最近,Paradigm 研究合伙人 Dave White、Dan Robinson 与 Uniswap 创始人 Hayden Adams 一起合作设计了一个全新的做市模型「时间加权做市商 TWAMM 」(The Time-Weighted Average Market Maker)。根据其发表文章介绍, TWAMM 可以在以太坊上有效地交易大额订单,工作原理是将长期大额订单分解为无限多个无限小的虚拟订单,在一定时间内使用嵌入式 AMM 平滑地执行这些交易。
关于 TWAMM 的虚拟交易所涉及的数学,Dave White 在文中并没有多费笔墨,只在最后给出了非常简单的数学结论,这对于理解 TWAMM 的数学原理非常不利。本文将重点对 TWAMM 的数学原理进行严格的论证和解释,至于 TWAMM 模型详细的设计原理,可以前往 Paradiagm 官网查看 ,本文不再做详述。
定义
假设 TWAMM 执行大额虚拟交易需要 N 个区块,出售 X 的池子以每区块 x rate 的速率出售,而出售 Y 的池子以每个区块 y rate 的速率出售。因此,在整个期间售出的 X 总量为 x in =Nx rate ,售出的 Y 总量为 y in =Ny rate 。
同时,我们将此时间段嵌入 AMM 的初始储备 x reserve 和 y reserve 分别表示为 x 0 =x ammStart 以及 y 0 =y ammStart 。
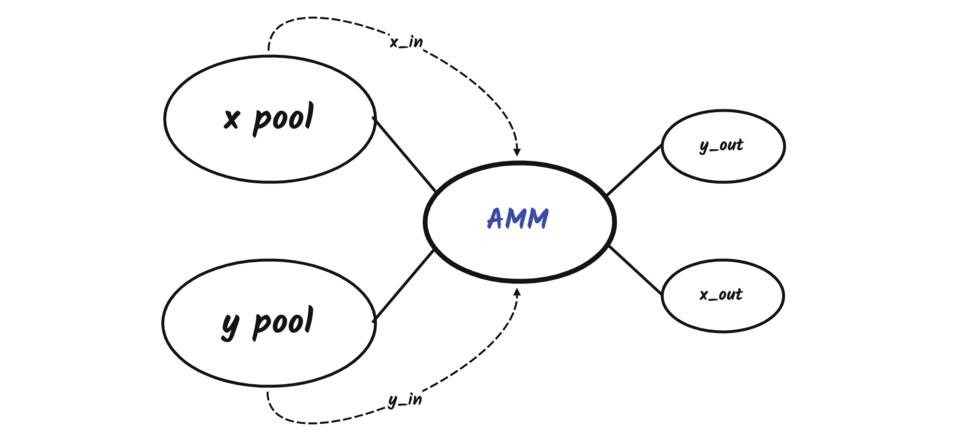
按照 TWAMM 的设计,大额订单是随着区块进行交易的,每个区块出售 x rate 得到 y out ,或者出售 x rate 得到 y out ,同时 AMM 会更新 x reserve 和 y reserve 的值,整个过程总共交易 N 次。
值得注意的是, AMM 的每个区块交易总是遵循恒定乘积做市。
公式
首先,在执行第 n-1 区块的交易后,我们假设此时 AMM 的 x reserve 和 y reserve 值分别为 x n-1 和 y n-1 。
接下来执行第 n 区块的交易,X-Pool 和 Y-Pool 分别向 AMM 输入 x rate 和 y rate ,命:
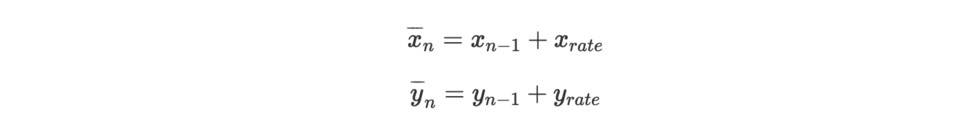
因为 x rate 和 y rate 非常微小,且区块的交易 AMM 遵循恒定乘积做市商,我们可以得到,
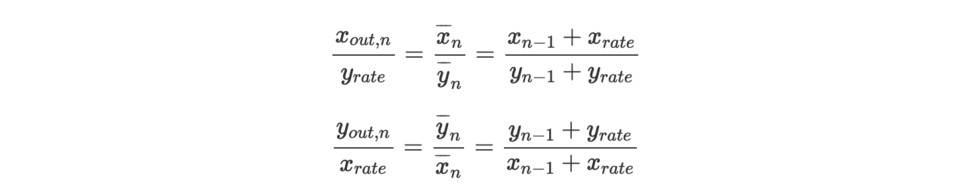
化简,
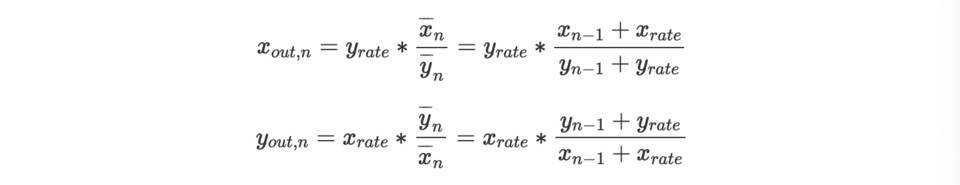
在得到 x out,n 和 y out,n 的值后,我们进一步可以获得 n 区块的交易后 AMM 的 x reserve 和 y reserve 值 x n 和 y n ,
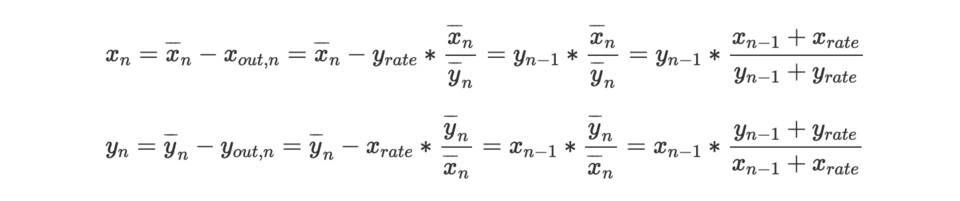
通过观察,我们发现 x n *y n =x n-1 *y n-1 ,这正好符合 AMM 的循恒定乘积做市的前提要求。
令, x n *y n =x n-1 *y n-1 =...= x 1 *y 1 =x 0 *y 0 =k,这是一个常数。
分式线性递归
先对 x n 求得一般公式,并获得 x ammEnd =x N 的值,y n 同理。
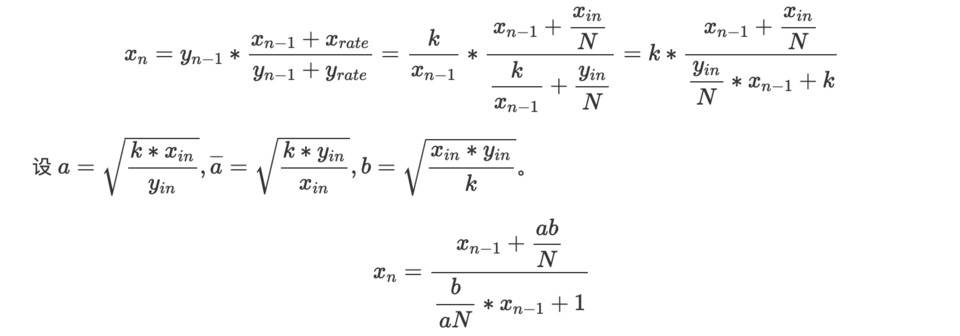
y n 的分式线性递归表达式如下:
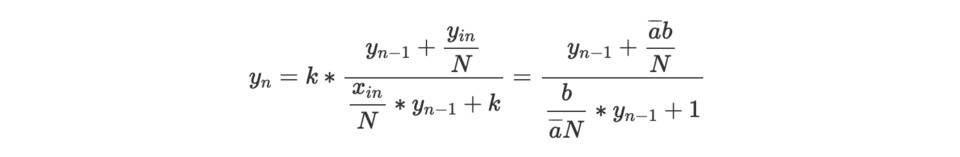
解
首先,若 y in 等于 0,x in 不等于 0,则
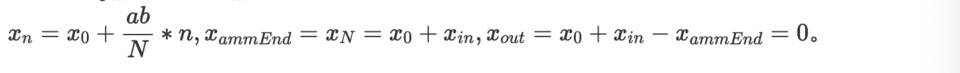
而
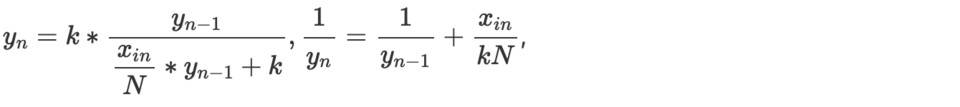
计算得到,
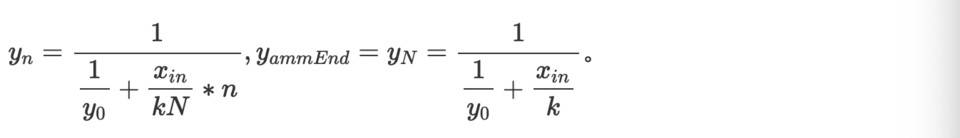
而,
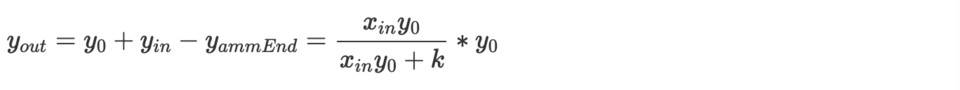
x in 等于 0,y in 不等于 0 时,讨论同上。
若 x in 和 y in 都不等于 0,对于一般的分式线性递归,我们可以采用 不动点 的方法求解。
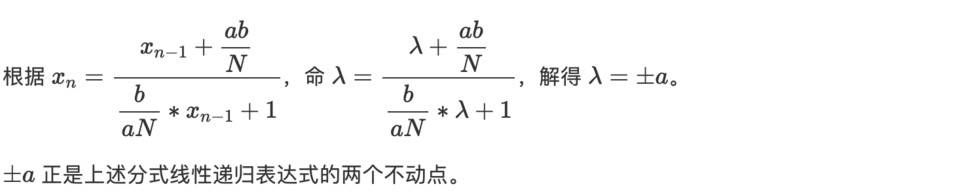
进一步计算,
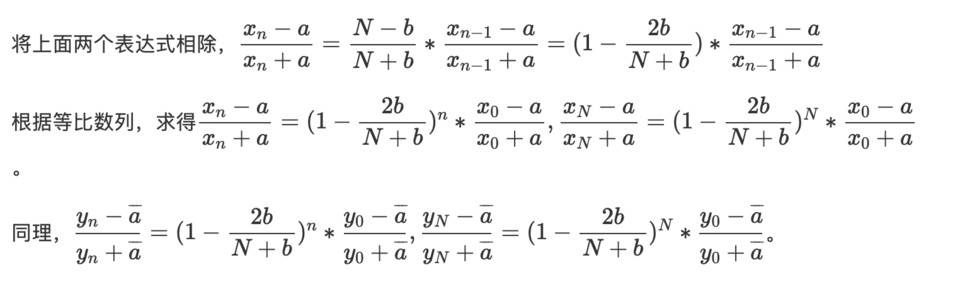
极限
TWAMM 的基本假设是将长期大额订单分解为无限多个无限小的虚拟订单,也即是 N 可以取无穷大,这时候可以获得 x N 的极限值。
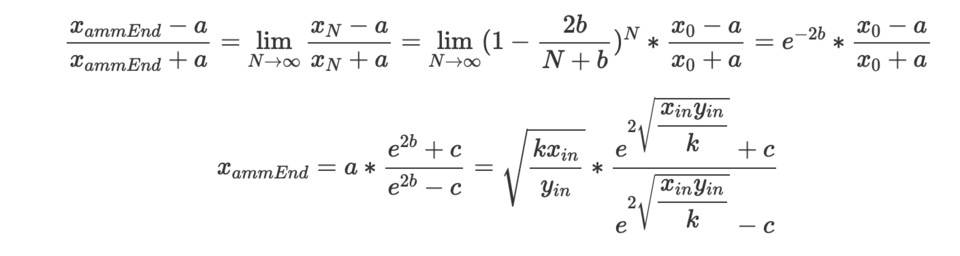
其中,
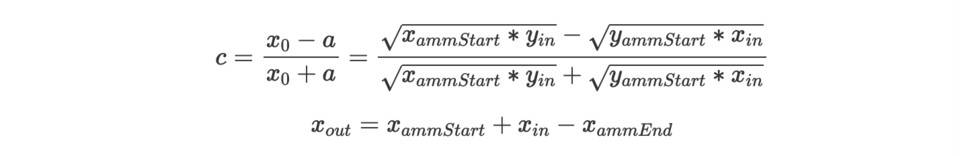
相似的,
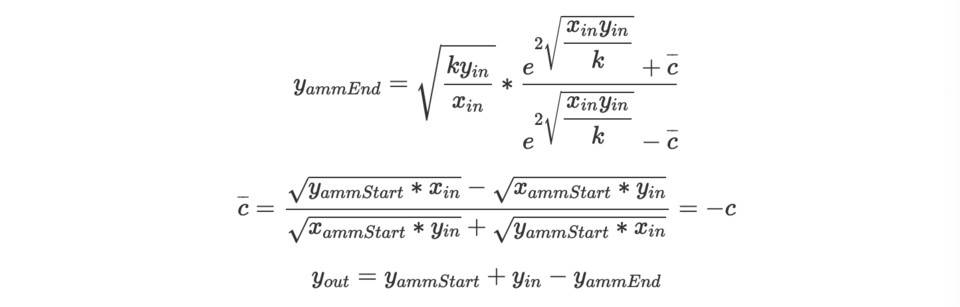
最后,经过简单的验证 x ammEnd *y ammEnd =x ammStart *y ammStart =k, 依然满足 AMM 的恒定乘积。
至此,我们完成了 TWAMM 的数学原理严格的论证和解释,并得到了与 「时间加权做市商 TWAMM 」 一文完全相同的结论。







