永恒期权为交易者提供了长期期权敞口,操作简单,也不需付出滚动头寸的费用。
撰文: Dave White 与 Sam Bankman-Fried,前者为加密资产投资基金 Paradigm 研究合伙人,后者为做市商 Alameda Research 和加密衍生品交易所 FTX 联合创始人
编译:Perry Wang
加密资产投资基金 Paradigm 研究合伙人 Dave White 与传奇交易员、做市商 Alameda Research 及加密衍生品交易所 FTX 联合创始人 Sam Bankman-Fried (SBF) 联合发表了一篇论文,介绍了一种新型金融衍生品,即永恒期权(everlasting option)。 按照该论文的说法,「永恒期权为交易者提供了长期期权敞口,操作简单、无风险,也不需付出滚动头寸的费用」。
Dave White 和 Sam Bankman-Fried 还为永恒期权推导出简单的无套利定价模型,可以适用于所有基于 funding fee 的永续衍生品,包括永续合约(perpetual future)。
期权基本知识
期权类型
文章伊始我们先向大家简单介绍一下最简单类型的期权:欧式期权(European option)。共有两种欧式期权:看涨(认购)期权 call option 和看跌(认沽)期权 put option。
看涨期权使期权持有人有权在约定日期的特定时间以约定价格(行权价)买进特定资产(标的物)。
看跌期权使期权持有人有权在到期时间以约定价格(行权价)卖出特定资产(标的物)。
举个例子
例如,5 月 15 日 3000 美元 ETH 看跌期权,意味着期权持有人在 5 月 15 日的特定时间有权以 3000 美元的价格卖出 1 个 ETH。
如果 5 月 15 日看跌期权到期时 ETH 的市场交易价格为 2900 美元,该期权持有人有权以 2900 美元从市场购买 1 个 ETH,然后通过这一看跌期权以 3000 美元价格立刻卖出,锁定 100 美元利润。这笔钱称为收益 (payoff)。
相反,如果 5 月 15 日看跌期权到期时 ETH 的市场交易价格为 3100 美元,该交易者在现货市场卖出 ETH 的价格高过执行这份看跌期权合约。在这种情况下,执行这份期权合约将不会带来收益,我们称这份期权的收益为 0。
收益计算
尽管欧式期权只有在到期日的特定时间可以被执行,或称行权(exercised),我们可以随时计算其收益。期权收益是衡量该期权如果立即执行会价值多少钱的度量。
通常,看跌期权的收益是 max(strike-spot, 0)。 当 ETH 交易的现货市场价格比行权价低得越多,通过看跌期权卖出 ETH 赚到的钱就越多。但是,如果 ETH 的现货市场价格高于到期时的行权价,那么直接在市场上卖出 ETH 要优于使用看跌期权,看跌期权就一文不值。
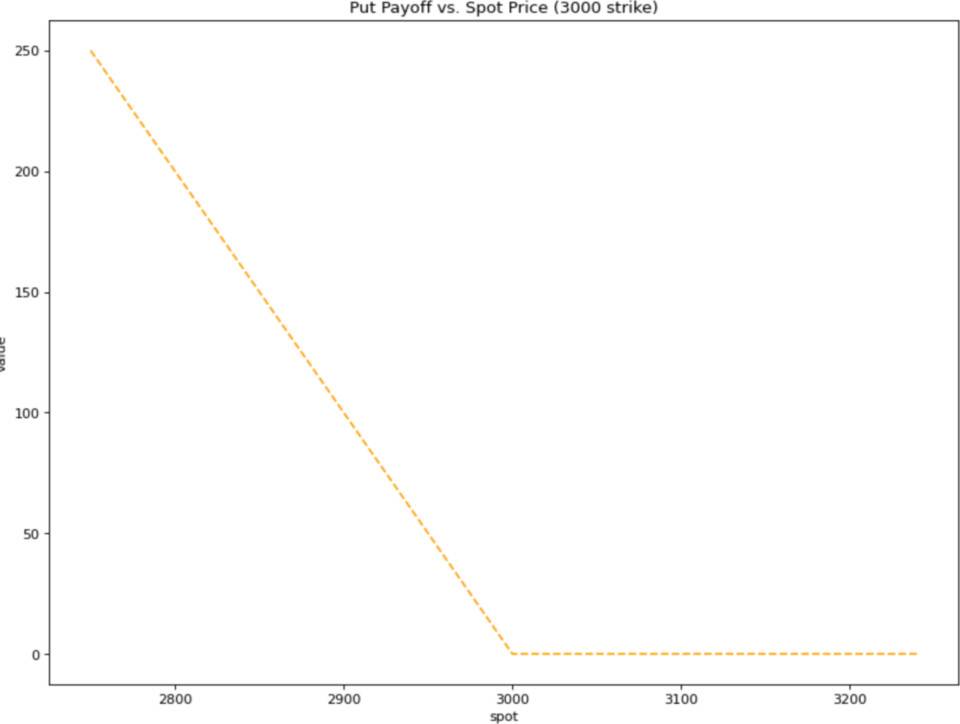
类似,一份看涨期权的收益是 max(spot – strike, 0)。如果 ETH 的现货交易价格为 3100 美元,而我们手中有到期时 3000 美元行权价买进 ETH 的看涨期权,我们可以行使该看涨期权以 3000 美元的价格买进 ETH,然后立即以 3100 美元的价格在市场上出售,获得 100 美元的收益。 但如果届时 ETH 的交易价格为 2900 美元,而我们手中 3000 美元行权价的 ETH 看涨期权则收益为 0 美元。
期权定价
在到期之前,期权合约的价格通常比其收益还高一些(不包括一些特殊情况)。
假设 3000 美元行权价的 ETH 看跌期权明天到期。如果 ETH 的价格当前市场价格为 3000 美元,则该看跌期权的当前收益为 $ 0。 但是 ETH 的价格可能会在明天下跌,在这种情况下看跌期权的到期价值将超过 0 美元。 因此看跌期权现在的价值必须大于 0 美元,才能覆盖这种可能性。
期权定价一种基本且广泛使用的模型是 Black-Scholes 模型。下图显示了行权价 3000 美元的 ETH 看跌期权到期前一天的 Black-Scholes 价格,与各种现货 ETH 价格的收益比较。
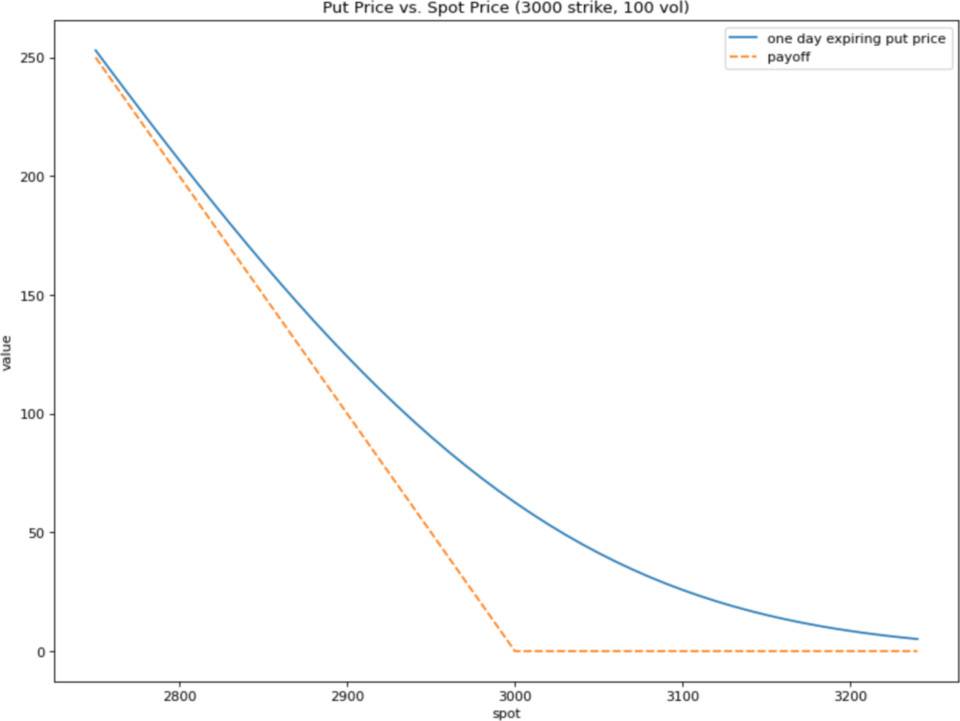
滚动头寸
定义
期权的主要用例是对冲或防范风险。例如,如果投资者持有大量的 ETH 投资仓位,则她可以选择购买足够的 3000 美元 ETH 看跌期权,以确保无论市场价格如何变化,她始终能够以至少 3000 美元 / ETH 的价格卖出头寸。
但是,这些看跌期权终究会到期。如果投资者想保持对冲,她将不得不滚动其期权头寸。在上述情况下,意味着平仓看跌期权中即将到期的头寸,并开设一个新的、行权价一样的看跌期权头寸,只是到期时间更靠后。
举个例子
例如,投资者最初可能买了 5 月 15 日到期的 3000 美元 /ETH 的看跌期权。当这些期权合约临近 5 月 15 日到期时,她可能会出售这些期权合约,并购买相同数量的 6 月 15 日 ETH 看跌期权,行权价仍为 3000 美元。只要她想保持自己的仓位,就必须每月重复一次这一过程。
问题
当投资者到市场上滚动头寸时,她很可能会与被称为做市商的市场参与者进行交易。
当信息不灵通的市场参与者(例如那些滚动期权头寸的交易者)与做市商交易时,做市商赚钱。 但是,做市商在与消息灵通的市场参与者(例如那些了解 ETH 价格新闻的参与者)进行交易时会亏本。
因为做市商不知道交易对手中谁是消息灵通谁是消息不灵通,他们必须对每笔交易收取一定的费用,称为价差 spread。 期权市场的价差往往特别高,因为在这种情况下,做市商的知情交易成本可能很高。 这使得滚动头寸的成本颇为昂贵。
滚动头寸还涉及工作和风险。交易者可能单纯只是忘了滚动,导致其头寸失去对冲。或者她可能会误点击或错误地执行交易,这可能既昂贵又危险。即使一切顺利,整个过程还是充满压力并且需要时间,使得投资者无法专注于更富有成效的工作中。
现有解决方案
现在市场中有一种称为永续美式期权(perpetual American option )的产品,该期权可以随时行权且没有到期日。卖出永续美式期权需要做市商预先承担大量的风险和不确定性,这使得它们既昂贵又难以定价。导致它们实际上从未交易过。正是因为该产品的存在,我们将新的替代品称为「永恒期权」。
流动性碎片化
如果存在许多不同的期权到期日,会导致另一个问题:流动性碎片化。如果做市商必须做市的标的不仅是本周到期的期权,还包括接下来的三个月中每个星期都有到期的期权,他们将被迫分散其资本,将使其他参与者更难进行大笔交易或确定公平价格。由于参与者必须决定对哪些到期日的期权进行交易,这个碎片化的市场也使得期权交易更加混乱。
期货市场类比
对传统上也有到期日的期货合约而言,所有这些问题也都会遇到。
如果交易者希望使用传统的到期期货来长期持有 ETH,那么她将不得不像选择期权那样滚动其头寸。例如,她可能会购买 5 月 15 日到期的 ETH 期货合约。然后在 5 月 15 日到期之前,她可能会卖出该合约并购买 6 月 15 日到期的 ETH 期货合约,依此类推。
就像选择期权一样,滚动其期货头寸需要时间、会带来风险,并要求她不断向做市商支付价差。 多个到期日期货合约的存在,还导致期货市场的流动性碎片化。
永续合约
BitMEX 于 2016 年面向加密货币推出的永续合约(Perpetual Futures )解决了这些问题。它们在不需要滚动的情况下,为交易者提供了期货风险敞口,持有时间任意。它们还将特定底层标的物的所有期货流动性集中在特定交易所的单一产品中。
永续合约已经变得大受欢迎,每天交易数百亿甚至数千亿美元的金额。
工作机制
简单说,永续合约的工作原理如下:每天那些做多(已买入)的交易者必须向那些做空者(已卖出)支付一笔融资费用。
这一融资费用的计算方式为(mark-index):标记价格 (永续合约的交易价格)与指数价格(标的物的市场价格,例如 ETH)之间的差额。
这种融资费用机制使永续合约的定价与标的物价格走势保持一致。粗略地说,如果永续合约价格比标的物市场价格高得多,那么多头将不得不支付高额的融资费用,这将激励他们卖出永续合约,从而降低其价格。
事实证明,我们可以得到比这更精确的结果。 有关永续合约的工作机制,请参阅 The Cartoon Guide to Perps 一文,或者参照下面列出的我们有关其准确估值的公式。
举个例子
如果 ETH 永续合约的当前为 3100 美元,而 ETH 的当前市场价格为 3000 美元,则多头必须向空头支付 「mark–index= 3100 美元– 3000 美元 = 每天 100 美元」。
如果 ETH 永续合约的价格为 2900 美元,而 ETH 的市场价格为 3000 美元,则 mark–index= 2900 美元– 3000 美元 =-100 美元,这意味着空头必须每天向多头支付 100 美元。
永恒期权
永恒期权等同于期权市场中的永续合约。
持有 3000 美元 /ETH 永恒期权的交易者始终可以以 3000 美元行权价格卖出她的 ETH。她将不得不支付融资费用,支撑自己的头寸,但是由于她不必持续与做市商进行交易,因此她无需支付价差或招致操作风险,除非进入和退出自己的头寸。
由于不再需要不同到期时间的期权合约,因此流动性的分散程度将降低,尽管在基础版本中,针对不同的行权价格,仍将有不同的永恒期货。
工作机制
永恒期权的工作方式与永续合约完全相同,只是有一个区别:融资费用的计算方法是标记价格与期权当前收益的差额,因此,funding fee 是(mark–payoff)而不是(mark–index)。
举个例子
以行权价 3000 美元的 ETH 看跌永恒期权为例,每天支付一次资金。
如果 ETH 当前的交易价格为 2900 美元,则看跌期权的当前收益为 3000 美元 – 2900 美元 = 100 美元。如果看跌永恒期权在支付融资费用之前的即刻交易价格为 150 美元,多头将向空头支付 mark–payoff= 150 美元– 100 美元 = 每天 50 美元。
如果 ETH 当前的交易价格为 3100 美元,高于永恒期权的价格,则看跌期权的收益为 0 美元。如果看跌永恒期权在支付融资费用前的即刻交易价格为 50 美元,多头将向空头支付 mark–payoff= 50 美元 – 0 美元 = 每天 50 美元。
请注意,行权价为 0 的 ETH 看涨期权,其收益就是 ETH 的市场价格,换句话说,payoff=index。 这意味着 0 行权价的永恒期权等同于 ETH 的期货。相应,0 行权价的永恒期权每日的融资费用为 「mark – payoff = mark – index」,与永续合约的融资费用相同。
定价
如果我们不知道永恒期权的价值,永恒期权就没什么用处。 幸运的是,通过以下列出的无套利论证,我们探索出了永恒期权的价值:它们等同于一个特定的、不断滚动的期权投资组合,因此其定价将与该投资组合相同。如果这两者价格的差异太大,套利者将介入以使其恢复一致。
假设每天支付一次费用,则该等价投资组合中一半为今天到期的期权合约,四分之一为明天到期的期权合约,八分之一为后天到期的期权合约,依此类推。所有这些期权合约的行权价都与永恒期权的行权价相同。
我们还可以创建一个单位时间内多次支付较小费用的永恒期权(例如,每小时支付 1/24 的费用),从而改变了等价投资组合的构成。有关详细信息,请参阅 报告 的附录 B。
无论哪种情况,我们都可以通过对这一篮子期权合约定价,以实现对永恒期权的定价。可以简单地通过获取各个期权价格的加权总和来完成(对小于投资组合中 1/1024 头寸的贡献进行估测)。 期权做市商完全有能力为这些单独的到期期权进行定价。
如果我们使用简单的 Black-Scholes 假设,它与现实世界的轨迹不匹配,但很接近。每天支付两次资金的永恒期权的轨迹几乎就像行权价格相同的一天后到期常规到期期权一样。
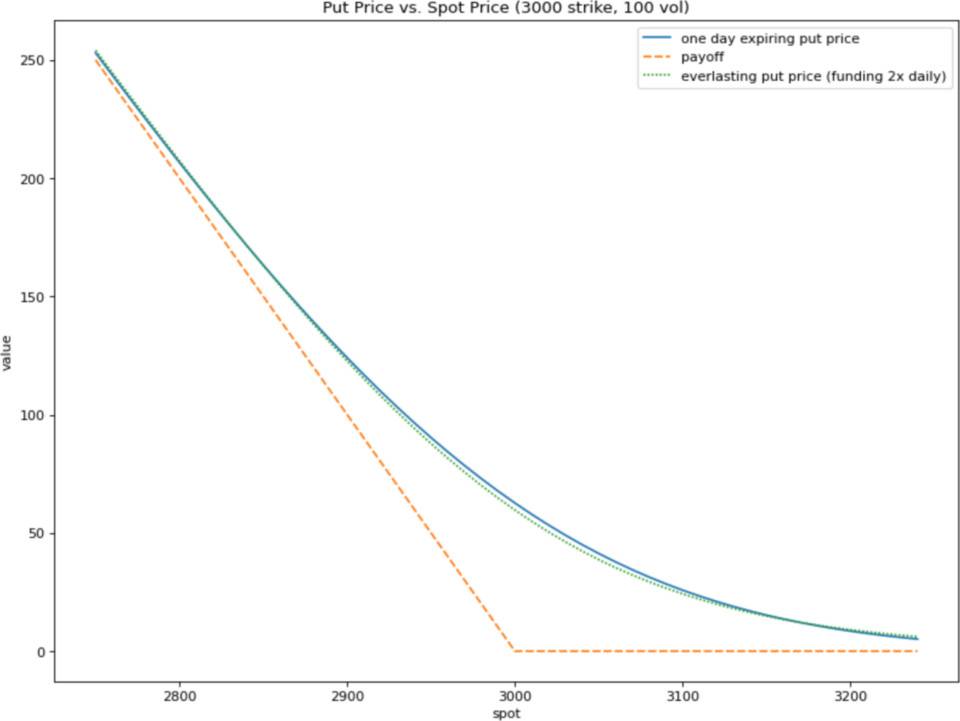
等效期权组合
融资费用支付所带来的价格影响
对永恒期权之类的基于融资费用的永续类衍生品进行合理的价格推定是难度很高的工作,因为它们的定价具有天然的不连续性。融资费用是在特定的准确时间(例如午夜)支付的。 就像股票支付股息一样,我们预测永续类衍生品的价格在支付融资费用后自然会立即上涨。
因此,尽管自然而然会想到「融资费用付款」的同时会发生其他事情,但结果都不尽人意 。在对永续衍生品在融资费用支付时间段的行为进行推理时,最好考虑一下在融资费用支付之前或之后会发生什么。
顺便说一句,在一定程度上当前的永续产品交易所在融资费用支付后不会自动更新其订单簿,就像证券交易所在股票分红后一样,意味着该市场面临套利损失的风险。 例如,如果多头是要向空头支付融资费用,则理性的交易者应在到期前一毫秒对其永续衍生品做空,拿到融资费用,然后在到期后一毫秒内买入以关闭其空头,从而以极小的风险收取利润 。
等效投资组合的直觉
描述
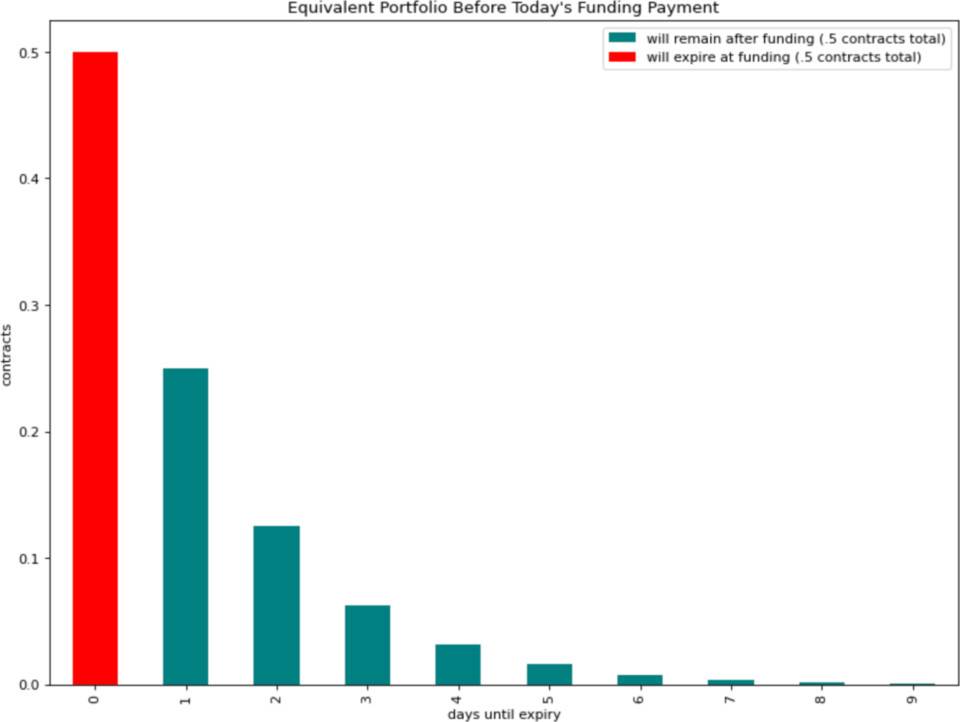
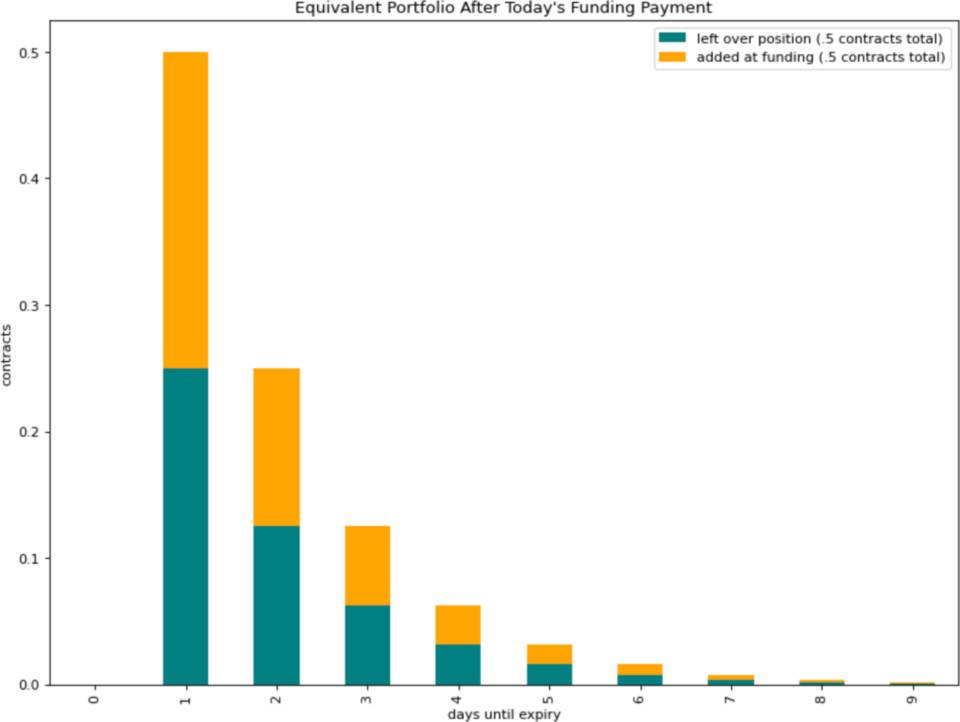
如前文所述,每天支付一次融资费用的永恒期权等同于定期到期期权的投资组合:一半为下次付款时到期的期权,四分之一为下一次费用交付时到期的期权,八分之一在再下一次付款时到期的期权,依此类推。该投资组合中的期权合约总数为一。
这意味着,在支付融资费用时,占总投资组合一半的期权合约已经到期。融资费用支付则对应于滚动投资组合的成本:购买期权合约总价值一半的新期权,以填补刚到期的一半合约。但是与手动滚动头寸的情况不同,这些新期权合约分布在多个到期日内,无需支付任何价差,也不会产生执行风险。
论证
假设,Alice 做多一份永恒期权,每天午夜支付一次融资费用。
Alice 必须在今晚午夜支付相当于 mark–payoff 的融资费用。让我们考虑一下现金流的含义。Mark 价格是在支付融资费用之前无限期购买永恒期权的成本,因此 Alice 支付了相当于她必须加倍其头寸所需要的费用。另一方面,由于 payoff 值为负,因此她会拿到 payoff,相当于她做多一份午夜到期的等效常规期权所获得的收益。
重复一遍,如果做多期权等同于部分常规期权的投资组合,则意味着 Alice 在到期前立即将其在每种期权中的头寸翻倍,然后在到期时获得相当于一份合约价值的 payoff。 这意味着直到她头寸翻倍之前,Alice 正好将合约的一半资产做多午夜到期的期权。
延伸这种思路,如果我们希望 Alice 的永恒期权等效组合在今晚之后继续运作,则她在常规期权中将于明日午夜到期的头寸,恰好是今晚翻番后合约的一半。只有在加倍之前其值等于期权合约的四分之一时才会保障情况如此……依此类推。
请注意,这一论证适用于具有确定收益的任何到期类衍生品,而不仅限于欧式期权。
论据
请参阅 报告 的附录 B。
延伸应用
通过对到期类衍生品定价,这一框架适用于对任何基于融资费用的永续衍生品定价,而不仅仅是限于欧式看涨期权和看跌期权。其中包括永续合约。
还包括二元看跌 binary put 期权,如果标的物价格高于给定的行权价格,则其收益为 0;如果低于行权价格则可获得 1 美元的收益,因此可以用作防范 DeFi 协议故障的缓冲。
浮动性行权价永恒期权
该框架还可适用于为浮动性期权定价,后者的行权价是标的物价格随时间变化的指数加权移动平均值。这是因为到期类等价组合(亚洲浮动期权)也可以定价,尽管定价难度极高。
拥有这样的看跌期权将始终可以有效地让 ETH 持币者能够以 ETH 的指数加权平均价格(半衰期为一天)出售其所持代币,保护其免受 ETH 价格突然暴跌的影响。
因为其行权价会自动跟随 ETH 的价格走势,所以单个此类产品有可能满足大多数 ETH 持币者的对冲需求。这有可能将许多 ETH 期权的流动性和交易额汇聚到一个市场中。
未来的工作
未来的工作主要是在应用领域。
- 永恒期权或其他以融资费用为基础的全新永续衍生品是否真正拥有市场?
- 哪种类型最有用?
- 如何最好地对它们进行参数化?
- 交易所和交易者如何才能最好地管理其风险?对于进行保证金交易的交易者,合适的清算标准是什么?
如果您对这些问题有任何想法,或需要提出自己的问题,我们将很高兴听取您的意见。
可以通过邮件地址 dave@paradigm.xyz 联络 Dave,或通过 Twitter 给他发私信,或 联络 SBF 。
鸣谢:感谢 Dan Robinson 在多次对话中为本文给予的直接和间接贡献;感谢 Hasu 给予的大量反馈,帮助本文澄清概念并梳理结构; 感谢 Georgios Konstantopoulos 对图片选择的中肯建议。
来源链接: www.paradigm.xyz







