DARMA Cash匿名公链技术(PLONK):改进的PLONK协议


PLONK 是Ariel Gabizon、Zac Williamson和Oana Ciobotaru公布了一种新的通用零知识证明方案,其全称是笨拙的“Permutations over Lagrange-bases for Oecumenical Noninteractive arguments of Knowledge”。 PLONK(以及更早但更复杂的SONIC以及最近的Marlin)带来的是一系列的优化,这些优化大大提高了零知识证明的可用性,在一定程度上解决了零知识证明的拓展性、安全性等问题。
原PLONK协议的优化
优化1:支持通用或可更新的可信设置(trusted setup)
虽然PLONK仍需要一个类似Zcash SNARKs的可信设置过程,但它是一个“通用且可更新”的可信设置。这意味着两件事:
首先,不需要为每一个你想证明的程序都设置一个单独的可信设置,而是为整个方案设置一个单独的可信设置,之后你可以将该方案与任何程序一起使用(在进行设置时可选择最大大小)。
第二,有一种方法可以让多方参与可信设置,这样只要其中任何一方是诚实的,那这个可信设置就是安全的,而且这种多方过程是完全连续的:首先是第一个人参与,然后是第二个人,然后是第三个……参与者们甚至不需要提前知道,新的参与者可以把自己添加到最后。这使得可信设置很容易拥有大量参与者,从而在实践中确保设置是非常安全的。
优化2:多项式承诺
它所依赖的“奇特密码学”是一个单一的标准化组件,称为“polynomial commitment”(多项式承诺)。PLONK使用基于可信设置和椭圆曲线对的“Kate commitments”(Kate承诺),但你也可以用其它方案替换它,例如FRI(这将使PLONK变成一种STARK)或者DARK(基于隐藏顺序组)。这意味着该方案在理论上与证明大小和安全性假设之间的任何(可实现的)权衡兼容。
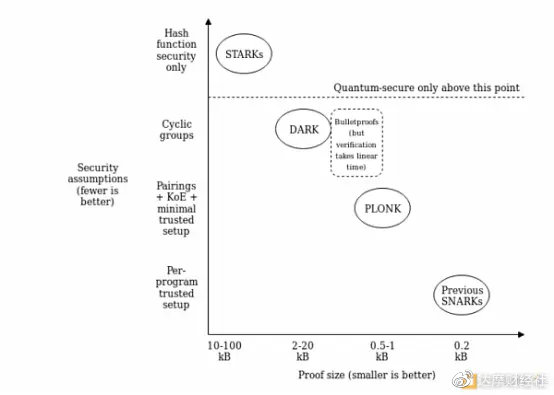
这意味着需要在证明大小与安全性假设之间进行不同权衡的用例(或者对这个问题有不同思想立场的开发人员),仍然可以为“算术化”共享大部分相同的工具(把一个程序转换成一组多项式方程的过程,然后用多项式承诺来检验)。
关于DARMA:改进的PLONK协议
DARMA 对PLONK协议进行了改进,取消了预信任的后门,采用STARK的FRI进行多项式验证,虽然损失了一部分效率,但是这让DARMA的零知识证明网络更加的安全且保护隐私,DARMA基于门罗并始终坚持保证每个用户的隐私。
DARMA:PLONK+FRI
PLONK的工作原理可以分为几部分:从线性系统到多项式—复制约束—合成多项式—多项式承若,DARMA使用FRI来进行多项式验证,解决了预信任问题,关闭了零知识证明的后门系统。
PLONK的工作原理
让我们从解释PLONK的工作原理开始,我们只关注多项式方程而不立即解释如何验证这些方程。PLONK的一个关键组成部分,就像SNARKs中使用的QAP一样,这是一个转换问题的过程,形式是“给我一个值X,我给你一个特定的程序P,这样当X作为输入进行计算时,给出一些具体的结果Y,” 放到问题“给我一组满足一组数学方程的值”当中。程序p可以表示很多东西,例如,问题可能是“给我一个数独的解决方案”,你可以通过将P设置为数独验证器加上一些编码的初始值并将Y设置为1 (即“是的,这个解决方案是正确的”)来对其进行编码,一个令人满意的输入X将是数独的有效解决方案。这是通过将P表示为一个带有逻辑门的加法和乘法电路,并将其转换为一个方程组来完成的,其中变量是所有线上的值,每个门有一个方程(例如,乘法为x6 = x4 * x7,加法为x8 = x5 + x9)。
下面是一个求x问题的例子,这样P(x) = x**3 + x + 5 = 35 (提示: x = 3):
我们按如下方式给门和线贴上标签:
在门和线上,我们有两种类型的约束:门约束(连接到相同门之间线的方程,例如a1 * b1 = c1)和复制约束(关于电路中任何位置的不同线相等的声明,例如a0 = a1 = b1 = b2 = a3 或者c0 = a1)。我们需要创建一个结构化的方程组,它最终将减少到一个非常少数量的多项式方程组,来表示这两个方程组。
在PLONK中,这些方程的设置和形式如下(其中,L = 左,R=右,O=输出,M=乘法,C=常数):
每个Q值都是一个常数,每个方程中的常数(和方程数)对于每个程序都是不同的。每个小写字母值都是一个变量,由用户提供:ai 是第i个门的左输入线,bi是右输入线,ci是第i个门的输出线。对于加法门,我们设置:
将这些常数插入方程并进行简化,得到ai+bi-oi=0,这正是我们想要的约束条件。对于乘法门,我们设置:
对于将ai设置为某个常数x的常数门,我们设置:
你可能已注意到线的每一端,以及一组线中的每根线,显然必须具有相同的值(例如x)对应于一个不同的变量;到目前为止,没有什么能强迫一个门的输出与另一个门的输入相同(我们称之为“复制约束”)。PLONK当然有一种强制复制约束的方法,我们稍后会讨论这个问题。所以现在我们有一个问题,证明者想要证明他们有一堆Xai, Xbi以及Xci值满足了一堆相同形式的方程。这仍然是一个大问题,但不像“找到这个计算机程序的一个令人满意的输入”,这是一个非常结构化的大问题,我们有数学工具可用于“压缩”它。
FRI
FRI的全名是”Fast RS IOPP”(RS = “Reed-Solomon”, IOPP = “Interactive Oracle Proofs of Proximity”)。藉由FRI可以达到简洁地验证多项式。
修改多项式维度
这一步是为了后面验证做准备的。在验证过程使用了一个技巧,将多项式以2的次方一直递减为常数项(D, D/2, D/4 … 1),大幅减低了验证的复杂度。因此,需要先将多项式修改为2^n维度
假设上述的每个限制多项式(不是合成多项式喔)为Cj(x),维度为Dj,D >= Dj 且D 等于2^n,为了达到D 维度,乘上一个维度(D -Dj)的多项式,
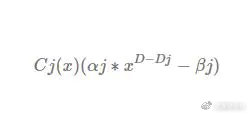
所以最终的合成多项式,如下
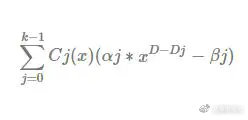
其中的αj、βj是由验证者(verifier)所提供,所以最终的多项式是由证明方(prover)跟验证方所共同组成。
*这小节的重点是将多项式修改成D维度,觉得多项式太烦可忽略
RS纠删码:
纠删码的概念是把原本的资料作延伸,使得部分资料即可以做验证与可容错。其方式是将资料组成多项式,藉由验证多项式来验证资料是否正确。举例来说,有d个点可以组成d-1 维的多项式y = f(x),藉由验证f(z1) ?= y,来确定z1是否是正确资料。
回到上面的问题,怎么证明知道多项式?最直接的方式就是直接带入点求解。藉由纠删码的方式,假设有d+1个点,根据Lagrange插值法,可以得到一个d 维的多项式h(x),如果如果两个多项式在(某个范围内)任意d 点上都相同( f(z) = h(z), z = z1, z2…zd),即可证明我知道f(x)。但是我们面对的是高维度的多项式,d 是1、2百万,这样的测试太没效率,且不可行。FRI 解决了这个问题,验证次数由百万次变成数十次。
降低复杂度
假设最终的合成多项式为f(x),藉由将原本的1元多项式改成2元多项式,以减少多项式的维度。假设f(x) = 1744 * x^{185423},加入第二变数y,使y = x^{1000},所以多项式可改写为g(x, y) = 1744*x^{423}*y ^{185}。藉由这样的方式,从本来10万的维度变成1千,藉由这种技巧大幅降低多项式的维度。在FRI 目前的实做,是将维度对半降低y = x²(f(x) = g(x, x²))。
此外,还有另一个技巧,将一个多项式拆成两个较小的多项式,把偶数次方跟奇数次方拆开,如下:
f(x)= g(x²) + xh(x²)
假如:
f(x) = a0 + a1x + a2x² + a3x³ + a4x⁴ + a5x⁵ g(x²) = a0 + a2x² + a4x⁴,(g(x) = a0 + a2x + a4x²)h(x²) = a1x + a3x² + a5x⁴,(h(x) = a1 + a3x + a5x² )
藉由这两个方法,可以将高维度的多项式拆解,重复地将维度对半再对半,以此类推到常数项。而FRI协议在流程上包含两阶段— 「提交」跟「查询」。
提交阶段:提交阶段就如同上述过程,将多项式拆解后,由验证者提供一乱数,组成新的多项式,再继续对多项式拆解,一直重复。
f(x) = f0(x) = g0(x²) + x*h0(x²) ==> f1(x) = g0(x) + α0*h0(x), ← α0(验证者提供)== > f2(x) = g1(x) + α1*h1(x), ← α1(验证者提供)==> . . .
查询阶段:这个阶段要验证证明者所提交的多项式f0(x), f1(x), f2(x), …是否正确,这边运用一个技巧,带入任意数z及-z(这代表在选域的时候,需满足L²= {x²:x ∊L},这边不多提)。所以可以得
f0(z) = g0(z²) + z*h0(z²) f0(-z) = g0(z²) -z*h0(z²)
藉由两者相加、相减,及可得g0(z²)、h0(z²),则可以计算出f1(z²),再推导出f1(x),以此类推验证证明者传来的多项式。
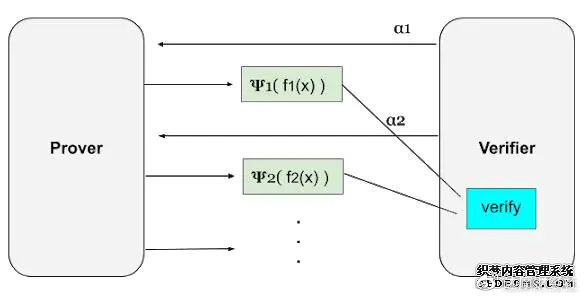
藉由FRI(RS纠删码、IOPs),将验证次数由数百万降至20–30次(log2(d)),达到了简洁地验证。不过,我们解决了复杂度,但还有互动性!






